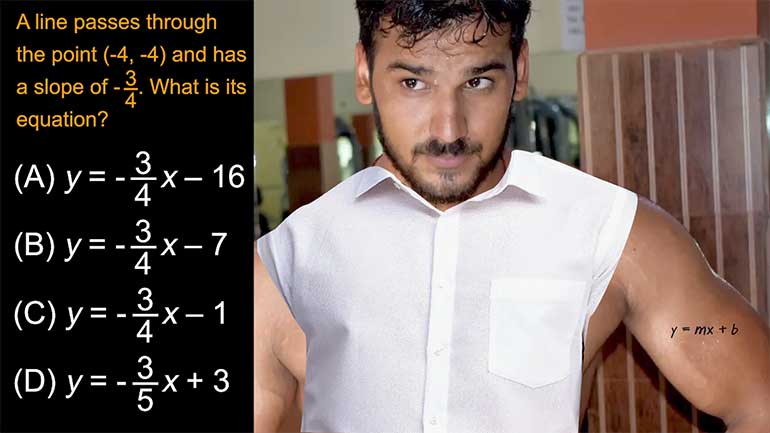ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
TSI Mathematics Videos 144 videos
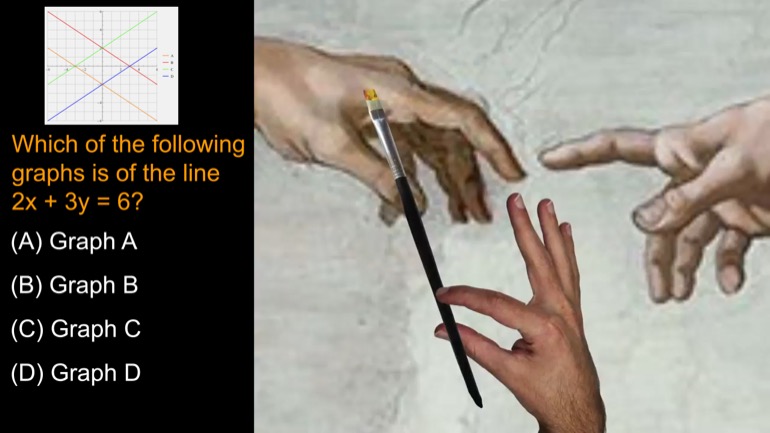
What is the equation of the line graphed above?
A line passes through the point (-4, -4) and has a slope of . What is its equation?
Line A has an x-intercept of -4 and a y-intercept of 8. What is its slope?
TSI Math: Finding a Range of Solutions for a Variable in a Triangle's Equation 45 Views
Share It!
Description:
What is the range of all possible values of x for ∆DEF, if DE = 2x – 7, EF = 3x + 9, and DF = 2x + 5?
Transcript
- 00:02
Okay next time for shoppers What is the range of
- 00:05
all possible values of x for angle df if d
- 00:10
is to explain a seven e f is three x
- 00:13
plus nine and gf is two x plus five Okay
- 00:20
interesting problem here Three lines have met forming a triangle
Full Transcript
- 00:24
and psych test takers everywhere are scrambling to determine a
- 00:27
little fact about this unholy union Like all heroes intent
- 00:31
on saving the universe from evil we need a strategy
- 00:33
Our strategy relies on the triangle inequality serum It says
- 00:37
that some of the lengths of any two sides of
- 00:39
a triangle must be greater than the length of the
- 00:42
third side Right Otherwise the triangle wouldn't touch so with
- 00:45
angle df we know that d plus e s greater
- 00:48
than d f e f plus d f is greater
- 00:50
than d e n d f plus d e is
- 00:52
greater than e f right So all the little side
- 00:55
thing he's touch will use this knowledge along with the
- 00:57
more algebraic definitions of the seides find all the possible
- 01:00
ranges of x let's start with d plus c f
- 01:03
his great of ndf and we'll get to x minus
- 01:05
seven plus three X plus nine is greater than two
- 01:08
x plus five But when we solve this inequality we
- 01:11
end up with yes x is greater than one right
- 01:14
Actually did all the math get point that x is
- 01:16
greater Next we have df plus cf scarier than d
- 01:19
e that gives us two x plus five plus two
- 01:21
extra stein's greater than to explain it's Seven solve it
- 01:24
and we get axes while greater than what is that
- 01:26
negative seven Yeah well this is obvious because we already
- 01:29
know that x is greater than once Of course it
- 01:31
has to be great the negative seven as well We
- 01:33
can't have a triangle with negative sides at least not
- 01:36
in this reality So lastly let's solve df plus de
- 01:39
is greater than e f and we get two x
- 01:41
plus five plus two extra money Seven is greater than
- 01:44
three x plus nine This will give us access great
- 01:46
event while eleven This inequality trumps the other two and
- 01:50
is the only one that matters and the value of
- 01:52
x can be anything It wants to be as long
- 01:55
as it's larger than eleven So the answer is d 00:01:57.456 --> [endTime] and yes we are shmoop oh snap
Related Videos
Which is the best way to revise and combine sentences 1 and 2?
Where would the following sentence best be placed?
Which of the following is best to insert at the beginning of sentence 8?
Which is the best location for sentence 9?
Which of the following sentences is best to insert between sentences 11 and 12?