ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Basic Geometry Videos 26 videos
SAT Math 1.4 Geometry and Measurement. If the sides of a square increase in size by 25%, what happens to the area of the square?
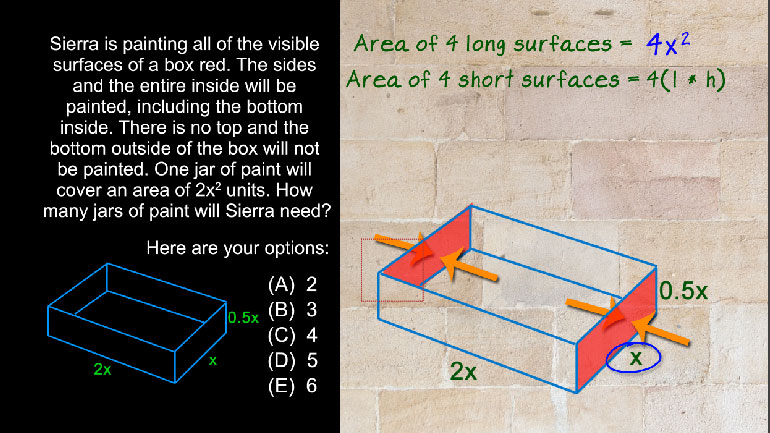
SAT Math 1.5 Geometry and Measurement. How many jars of paint will Sierra need?
Surface Area of a Cube 5082 Views
Share It!
Description:
Good thing surface areas are as easy as they seem on the surface.
Transcript
- 00:06
Surface of a Cube, a la Shmoop. Harold the hobo would like to cover his new
- 00:12
box while he sleeps at night...
- 00:14
...so no one sees it and tries to steal it.
- 00:18
Harold's not the smartest knife in the drawer. Man, he sure wishes he had a drawer.
- 00:23
Assuming Harold knows the volume of the cube is 1,728 milliliters...
Full Transcript
- 00:27
...how much material will he need to make a perfect-fitting box cozy?
- 00:32
We can use the cube's volume to help Harold figure out its surface area.
- 00:37
Here are our choices:
- 00:39
First, let's break down that box. We can start by working backwards.
- 00:46
We know that the volume of our cube is 1,728. So now we need to work backwards.
- 00:51
Volume is length times width times height.
- 00:54
Lucky for us, all are the same length in a cube.
- 00:57
To find volume, we can raise length, width or height to the third power... or cube it.
- 01:04
So we simply need to take the cube root of the volume.
- 01:07
The cube root of 1,728 is 12.
- 01:18
There's our length, width and height.
- 01:22
Now let's find the surface area of one side.
- 01:25
Multiply the box's width by its height.
- 01:27
So that is 12 times 12, which gives us 144... How many sides are there again, Harold?
- 01:34
Yep... six of 'em.
- 01:37
So 144 times 6 equals... 864.
- 01:42
Choice E, you're the winner!
- 01:44
Now Harold has enough material to hide his home...
- 01:48
...and doesn't have to worry about some box-thief filching it in the night.
- 01:59
Sleep tight, Harold. Don't let the literal bed bugs bite.
Related Videos
Haven't you always wondered how much cardboard it takes to encase a trunk warmer for your pet elephant?
Es una cosa cuando todas esas figuras geométricas están puestas en un pie de la página, pero cuando estas empiezan a expanderse y a invader nues...
Does thinking about 3D Geometry get you bent out of shape? Never fear! Watch this video and figure out some fun new shapes to bend back into. We're...
ACT Math: Plane Geometry Drill 1, Problem 5. If two polygons have the same shape and size, they are what?