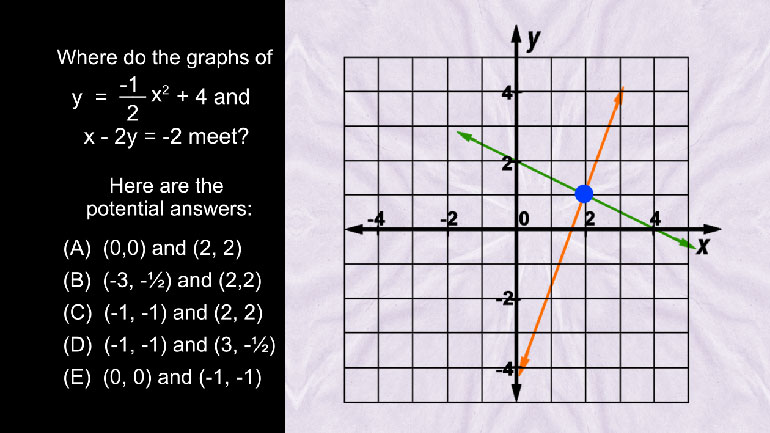
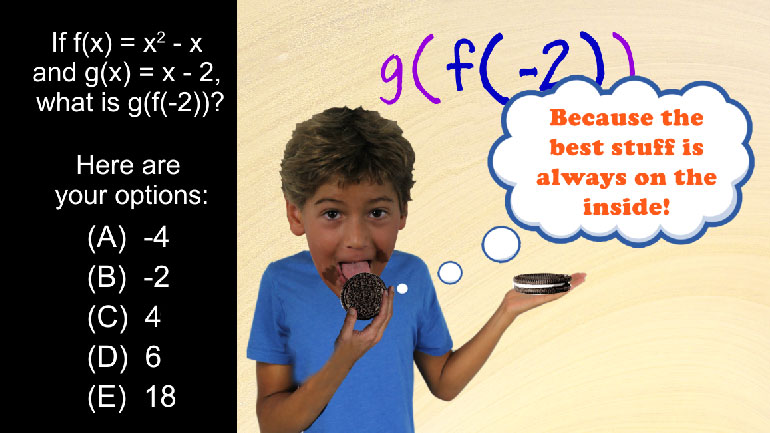ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
SAT Math 3.3 Algebra and Functions 182 Views
Share It!
Description:
SAT Math 3.3 Algebra and Functions
Transcript
- 00:02
And here's your shmoop du jour...
- 00:04
Justin rode his bike to school, pedaling at an average speed of 12 miles/hour.
- 00:08
When he rode his bike back home at a leisurely pace of 10 miles/hour, it took him an extra 15 min.
- 00:14
How far is his school from his home?
- 00:17
And here are the potential answers...
Full Transcript
- 00:20
OK, we want to find the distance between Justin's home and his school.
- 00:24
We know that he biked to school at 12 miles per hour, but we don't know how long it
- 00:28
took him to get there. We'll call the time it takes him to bike there, x.
- 00:33
Next, we know that when coming home, he biked at only 10 miles per hour.
- 00:38
And it took him 15 minutes longer than before.
- 00:43
We can take the old time, add 15 minutes to it, and get the new time.
- 00:48
But wait.
- 00:48
His velocity is given in miles per hour, and the extra time is in minutes.
- 00:54
The units don't match up.
- 00:55
Remember that 60 minutes are in an hour, and 15 minutes is .25, or a quarter of an hour.
- 01:01
Now, we can set up equations that help us solve this problem.
- 01:04
We'll start with biking to school.
- 01:06
We know that velocity is equal to the distance Justin travels divided by
- 01:09
the time it takes him to travel that distance. His velocity is 12 miles per hour.
- 01:14
We get the equation 12 = d (distance) / x (time).
- 01:18
Okay, now biking home.
- 01:20
We get 10 = d over the quantity x + .25.
- 01:26
We have two equations, and two variables.
- 01:28
Sounds a little like we have to solve a system of equations.
- 01:32
By isolating x in the first equation, we get x = d/12.
- 01:35
We can then plug x into our second equation, like this.
- 01:39
We multiply both sides by d/12 + .25, and we get 10 times d/12 + .25 = d.
- 01:47
Distributing in the 10 we get 10/12 d + 2.5 is equal to d.
- 01:54
We then subtract 10/12d from both sides to get 2/12 d,
- 01:59
which we can simplify to 1/6 d is equal to 2.5.
- 02:03
Finally, multiplying both sides by 6, and we get that d is equal to 15 miles.
- 02:08
So our answer is (E).
Related Videos
SAT Math 2.1 Geometry and Measurement. What is the measure of angle z in terms of x and y?
In 2014, the unemployment rate of one county in California was 7%. In another county, the unemployment rate was 11%. Which of the following express...
Angela is making cookies for a bake sale. She expects each batch of her cookies to sell for $40. It costs her $10 to make one batch of cookies, and...