ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Parallel and Perpendicular Lines Videos 23 videos
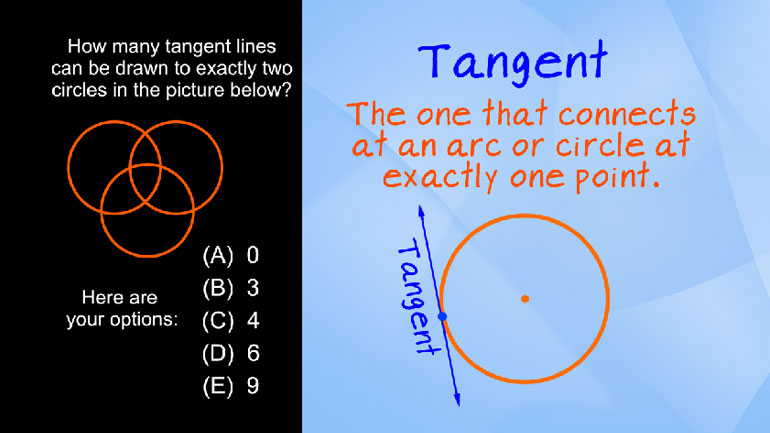
SAT Math 2.1 Geometry and Measurement. What is the measure of angle z in terms of x and y?
SAT Math 11.4 Geometry and Measurement. What is the y-intercept of a line parallel to y – 2x = 4 and passing through the point (1, 2)?
CAHSEE Math 4.5 Algebra I 229 Views
Share It!
Description:
Algebra I Drill 4, Problem 5. What is the slope of a line that is parallel to the graph of 8x + 4y = 5?
Transcript
- 00:03
You look like you could use a little more shmoop in your life…
- 00:06
What is the slope of a line that is parallel to the graph of 8x + 4y = 5?
- 00:12
Here are the potential answers…
- 00:19
So… what is this question asking?
- 00:20
Can we take this jumbled mess and mold it into something we can work with?
Full Transcript
- 00:24
Namely… into the form of y = mx + b? Let’s give it a shot.
- 00:30
First we need to switch the order of the terms.
- 00:32
When we subtract 8x from both sides, we get 4y equals negative 8x plus 5.
- 00:40
Then we need y to stand alone – so we divide both sides by 4
- 00:44
to get y = -2x plus 5 fourths.
- 00:49
Our slope is negative 2.
- 00:51
But the question asks for the slope of the line PARALLEL to this one.
- 00:55
Oooh – trick question, kinda. Parallel lines all have the same slope.
- 00:59
So… nice try, but we’re onto you, Mister Problem Maker.
- 01:03
Our slope is negative 2, meaning the line slopes downward like this…
- 01:09
So our answer is A. As in, "Avalanche."
Related Videos
CAHSEE Math: Algebra and Functions Drill 5, Problem 3. Solve the equation.
This video explores parallel lines and transversals: how to identify them both on a math test and in real life urban planning. What do the consecut...
To prove lines are parallel, you need a third line. We at Shmoop (and the rest of the world) call it a transversal.
A sequel to the 1989 classic Segments, Lines, and Videotape, this video will change the way you think about lines, segments, and rays. Unless yo...