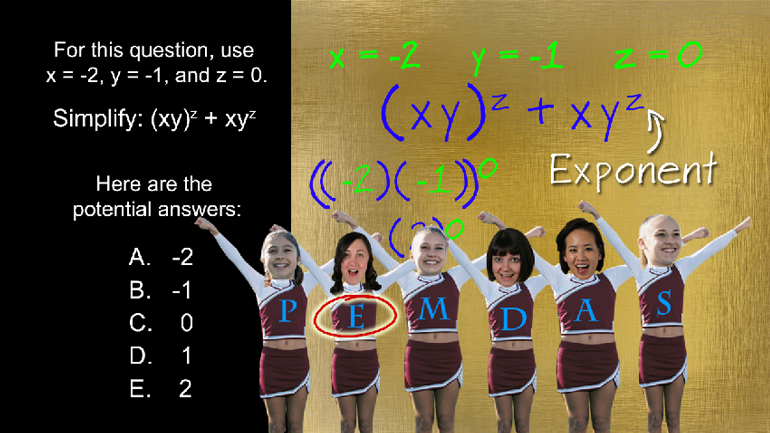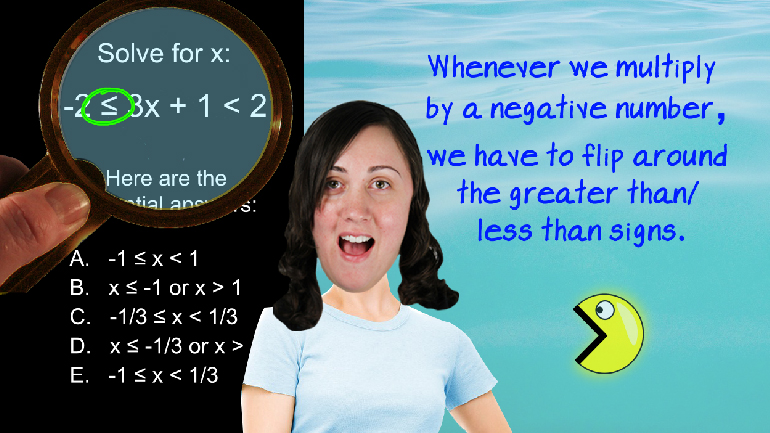ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Elementary Algebra Videos 26 videos
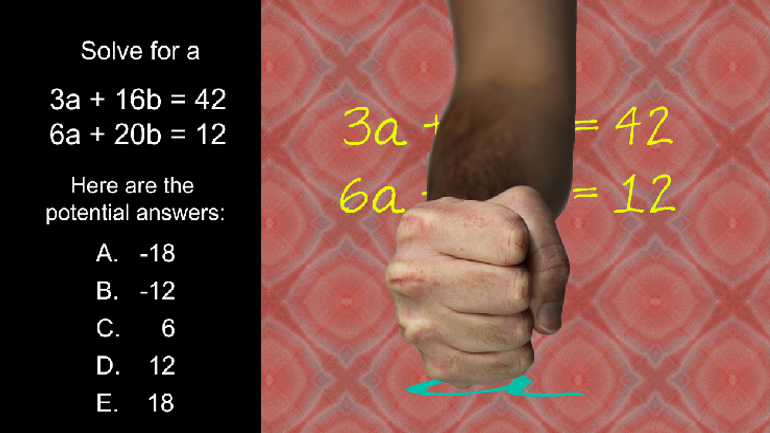
Elementary Algebra Drill 2: Problem 2. Can you find the product?
Elementary Algebra Drill 2: Problem 4. Factor the expression.
ACT Math 4.2 Elementary Algebra 301 Views
Share It!
Description:
ACT Math Elementary Algebra Drill 4, Problem 2. Solve for x.
Transcript
- 00:02
Time for your daily dose of Shmoop. This won't hurt a bit.
- 00:06
Solve for x: the absolute value of x plus 1 all over 2... is less than 3.
- 00:12
And here are the potential answers...
- 00:19
It's yet another absolutely fabulous... absolute value question.
- 00:22
Let's start by ignoring the absolute value lines and solve as if they were all positive numbers.
Full Transcript
- 00:28
We multiply both sides by 2 to get x plus 1 is less than 6.
- 00:32
Subtract 1 from both sides and we have x is less than 5, so our potential answers are
- 00:36
only B and C.
- 00:38
Now let's figure out what this problem would be if x were the most negative it could be.
- 00:43
What would make things under the absolute value lines to equal NEGATIVE 3?
- 00:47
We'd have x plus 1 over 2 is less than negative 3, but with no absolute value lines now.
- 00:53
We multiply both sides by 2 and we have x plus 1 is less than negative 6.
- 00:57
Then subtract 1 from both sides and we have x is less than negative 7.
- 01:01
So we have a positive 5 and a negative 7 as the range here.
- 01:05
Which is... this range... and our answer is C.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
It's impressive that these expressions are able to stay so rational even when they're having operations performed on them.
Jack and Jill went up the hill to fetch a pail of water. But what happened when they got up there? They’ve been gone an awfully long time…