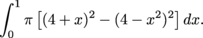Answer
The region R looks like this:
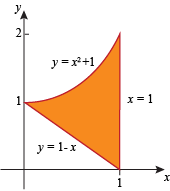
(a) When we rotate the region R around the line y = 0 we get the solid
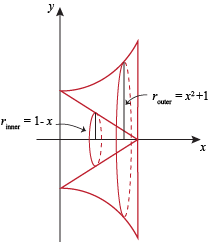
We can see from the picture that the outer radius is the distance from the x-axis to the graph y = x2 + 1, and the inner radius is the distance from the x-axis to the graph y = 1 – x.
So
router = x2 + 1
rinner = 1 – x.
Since the thickness of a disk is dx, the volume of the disk is
π[(x2 + 1)2 – (1 – x)2 ] Δ x.
There are disks from x = 0 to x = 1. The volume of the solid is
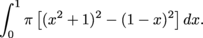
(b) When we rotate R around the line y = 2 we get
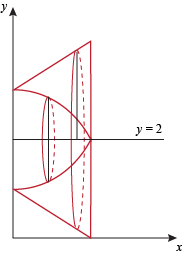
The outer radius is the distance from the graph y = 1 – x to the axis of rotation y = 2.
This distance is
router = 2 – (1 – x) = 1 + x
The inner radius is the distance from the graph y = x2 + 1 to the axis of rotation y = 2
This distance is
rinner = 2 – (x2 + 1) = 1 – x2
This means the volume of a disk is
π[(router)2 – (rinner)2] Δ x = π[(1 + x)2 – (1 – x2)2 ] Δ x
Put the pieces together, we get the volume of the solid:
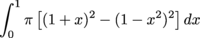
(c) When R is rotated around the line y = -2 we get the solid
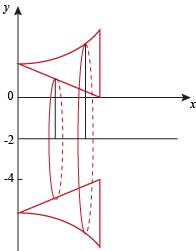
The outer radius is the distance from the axis of rotation y = -2 to the graph y = x2 + 1.
This distance is
router = (x2 + 1) + 2 = x2 + 3.
The inner radius is the distance from the axis of rotation y = -2 to the graph y = 1 – x.
This distance is
rinner = (1 – x) + 2 = 3 – x.
The volume of a disk is
π[(router)2 – (rinner)2] Δ x = π[(x2 + 3)2 – (3 – x)2 ] Δ x,
and the volume of the entire solid is
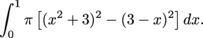
(d) Rotating R around the line y = 5 produces a solid with a very large hole in the middle.
Let's see if we can do this one without a picture.
The outer radius is the distance from the axis of rotation y = 5 to the graph y = 1 – x.
This is
router = 5 – (1 – x) = 4 + x.
The inner radius is the distance from the axis of rotation y = 5 to the graph y = x2 + 1.
This is
rinner = 5 – (x2 + 1) = 4 – x2.
The volume of a disk is
π[(router)2 – (rinner)2] Δ x = π[(4 + x)2 – (4 – x2)2 ] Δ x.
and the volume of the entire solid is