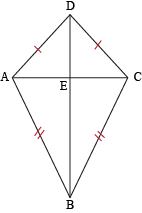
This one's got a lot of information, so let's break it down. Literally. We won't digest it or anything, though. We'll separate the kite into four right triangles: ΔPZH, ΔIZH, ΔIZL, and ΔPZL. The perimeter of the kite is the summed up lengths of all the hypotenuses. Since some are congruent to each other, though, we only need to find two hypotenuses. So let's start with ΔPZH. Since we know that IP is the cross diagonal, point Z is its midpoint. In other words, we know that PZ = IZ = 9 cm. With the knowledge that ZH = 40 cm, we can use the Pythagorean Theorem to find PH. a2 + b = c
92 + 402 = PH 2
81 + 1600 = PH 2

PH = 41 This means that PH = 41 cm long. Of course, since PH ≅ IH, we know that IH = 41 cm, too. Two sides down; two to go. Now, let's look at ΔPZL. We can't really use the Pythagorean Theorem to find the length of PL because we have no idea how long LZ is. If we had the total length of LH we could figure it out, but we're out of luck on that front. Wave goodbye to Pythagoras and say hello to trigonometry. Yes, that's right. Trigonometry: the apple of your eye. Or more like the pain in your neck. It won't be that bad. As long as we remember a few simple definitions, we'll be fine. In ΔPZL, we only know that ∠PLZ has a measure of 37° and PZ = 9 cm. We want to find the value of PL, so let's choose the right trigonometric ratio for the job. If PZ is opposite the angle and PL is the hypotenuse, we want to use sine. (Confused? Don't forget the wonders of SOHCAHTOA.) 



PL ≈ 15 cm Sweet. We've not only found the length of PL, but the length of LI as well. They're congruent, remember? The final step is just to add all our values together. In other words, P = 41 cm + 41 cm + 15 cm + 15 cm = 112 cm. That's our perimeter, and we're sticking to it. |