Area Formulas at a Glance

Let's go over these area formulas one more time.

Area of a Rectangle = Base × Height

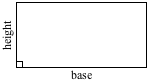
Area of a Square = Base × Height

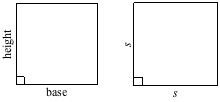
Area of a Square = s²

A square, technically speaking, is a rectangle (don't remind the rectangle, it's a little sensitive), so we can use the formula for the area of a rectangle to find the area of a square. Since a square's base and height are equal, the area of a square is also side length times side length, or side length squared. We're way too lazy to write out "side length" so we're going to abbreviate it as s, which makes Area = s².

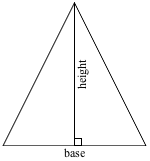
Area of Triangle = ½(Base × Height)

The height of a triangle is the length of a line that connects the base and vertex and is perpendicular to the base. So, the height has to square up with the base.

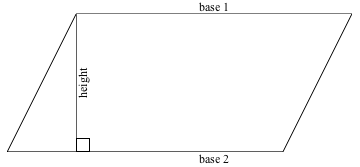
Area of Parallelogram = Base × Height

The height of a parallelogram goes from one base to the other and has to meet both bases at right angles.

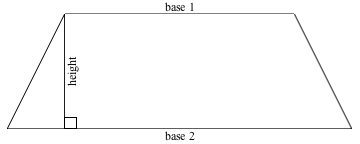
Area of Trapezoid = ½(Base₁ + Base₂) × Height

The height of a trapezoid, like the height of a parallelogram, is the distance between the two bases

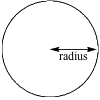
Area of Circle = π(radius)² = πr²

Pi, or π, is the ratio of the circumference to the diameter and is an irrational number. What we need to remember for the formula, though, is that π is often rounded to 3.14.