The Durbin Watson Statistic lets us know when good statistical regression analysis has gone bad...like a donut that looks good on the outside, but is actually super stale. Nobody likes a stale donut.
The Durbin Watson Statistic tests a time-series regression for autocorrelation, which we don’t want. Other tests might say “hey, you, your regression is looking good!” while the Durbin Watson Statistic test might say “uhmmm, actually, you should take another look...something’s not right, even if the others tests checked out.” The Durbin Watson Statistic gives a value of 2 if there’s not autocorrelation, or a value above or below 2 (within 0 - 4 range), which means there’s negative or positive autocorrelation.
So what is autocorrelation, and why is it bad? Regressions are functions that try to use a bunch of data to predict something. Basically, regressions are a statistical method to find correlations (it can’t prove causations, though...for that we’ve gotta have experiments) by fitting data to a line. Finding the best line for the data is the goal. How far the data points are from the line is the error, which we want to minimize to get the best fit line.
When there’s autocorrelation, that means your error value of your regression is correlated, either negatively or positively. If your regression “fits” the data well and your errors are correlated, that means something’s wrong. For instance, it could mean that you missed a really important variable that has some explanatory power, which shouldn’t be nested in your error, but a part of your regression line (omitted variable bias).
You can also get autocorrelation when your regression is functionally misspecified, which means your regression doesn’t actually fit the data well, because you have equal errors on both sides of your regression line, showing that you missed something in the relationship...which is kinda the point of doing a regression.
A third way you can get autocorrelation is measurement error in the independent variable, which will cause your independent variable and your error variable to both reflect that measurement error, and you’ll find your errors correlating over time with that measurement error.
Related or Semi-related Video
Finance: What are correlation coefficien...37 Views
Finance allah shmoop what are correlation coefficients Kind of sounds
like a new card game from the makers of cards
against humanity or an exotic disease that spreads like wildfire
on a cruise ship you know been there But a
correlation coefficient is actually a measure of how strongly connected
or correlated to different variables are It's also a measure
of how close the points on a scatter plot are
to the vest Fifth line this thing running through them
A correlation coefficient is kind of like a ranch hand
who's in charge of hurting data Okay so let's take
a closer look at the data points in our corral
taken from wild pizza restaurant Yeah they're a set of
by vary it or to variable data In this case
the data points on the x axis are the number
of minutes a table has to wait for their food
since ordering and the data points on the y axis
are the percentage of the total bill left as a
tip Interesting correlation here Pete the owner namesake of wild
pete's pizza believes there's a relationship between how long a
table waits for the food and how much they tip
generally the first step in finding a correlation coefficient is
to determine if the data points are in a roughly
leaning your pattern So we need to whip up a
quick scatter plot like this thing If the data points
don't have an obvious linear pattern lily shouldn't even bother
to calculate the correlation coefficient because it's not meaningful Once
there appears to be a linear or roughly linear pattern
to the data it's time to get calculate their partner
okay The formula for the correlation coefficient which is denoted
by the variable are here was a bit unwieldy and
typically the correlation coefficient calculated using an actual calculator of
some kind But still it's nice to know where these
numbers come from so we'll do it by hand and
double check our work So the process goes like this
First we find the mean in standard deviation in the
ecs data in the wide out of treating each set
of data as its own list separate from each other
We'll use a calculator just a shortcut this part of
the process and now we need to take its data
point in the x list Subtract the mean from it
and divide that result by the standard deviation so twelve
months fifteen point one six six seven which is negative
Three point one six seven divided by five point six
blah blah blah which is negative about a half then
twenty minus fifteen point one six seven which is four
point eight three three divided by five points You bubba
blah blah blah which is point eight six and change
and so on But we need the lather rinse Repeat
that same process of subtracting the mean of the y
data from each y value and then dividing the standard
deviation in the y values Right Well that'll be sixteen
months Fourteen which in california is too divided by three
point two eight blah blah blah which is point six
and change So we have thirteen months fourteen which is
negative one divided by three point two eight six which
is well negative point three ish So now we need
to multiply each matched acts And why value from our
previous calculations That'll be negative Point five six and change
times a point six blah blah blah which is negative
Point three four for one Then we have point eight
six three times negative point three oh four which is
a negative point two six two Then negative point seven
four four times one point two one seven two which
is Well what is that Negative point nine and so
on Now he's some the values we just got which
is all this stuff We adam all up and it
comes out to negative Four point four five five four
Okay one last step here Cowpokes We just need to
divide one less than the number of data points We
have six data points So we divide by negative Four
point four five five four yeah by five Divide that
And that means our correlation coefficient or our value is
negative Point eight nine one one Interesting Excellent Well now
we have a real correlation coefficient also What does it
mean Well for starters we can interpret what it actually
means here Say we did their correlation coefficient or our
value is a measure of how strong your relationship is
between the two variables Assuming that linear ish pattern exists
It does not however mean that the one variable causes
the other It just means there's some kind of relationship
between them toe actually put a value on how strong
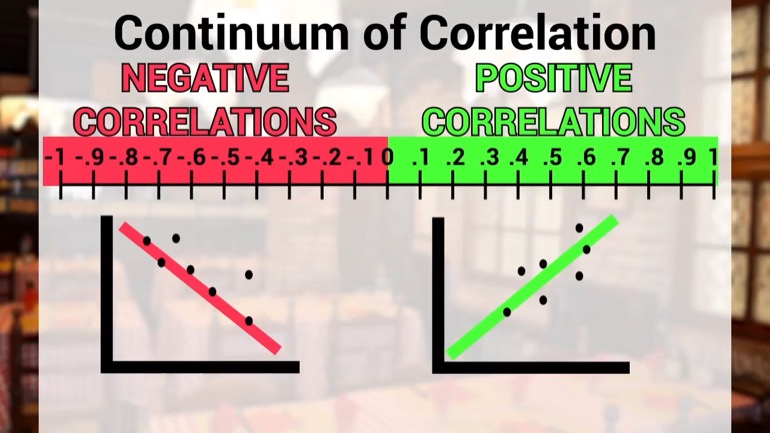
the correlation is We need to examine the continuum of
correlation Positive correlations represent situations where the scatter plot appears
to climb from left to right Negative correlations represent situations
where the scatter plot appears Toe fall from left to
right like our tips versus time data Well strong correlations
or values between point seven and one for positive correlations
and between negative point seven and one four negative correlations
That's just rough Numbers They're about point 7 And if
it's a one to one relationship it means that if
you let go of the apple it will fall every
time we're assuming they're on earth Scatter plot points will
be pretty darn close to the best fit line through
the points there medium correlations are in the point for
two point seven range and they got the negative ones
And so on Scatter plot points will be a we
distance from the best fit line Then it's not White
is tightly packed around that line and then we correlations
and just looks like a cloud It's like values from
zero two point for and zero negative point for and
they're just kind of like maybe there's a line through
there but maybe not well in our case it's our
our value is negative point eight nine one one While
it's very very negatively correlated between the two time of
ordering the food and when it shows up and the
tip paid at least the tip percentage of the meal
Which means that as it takes longer and longer for
food to arrive after ordering in general the tip percentage
goes down Also because this pattern is a strong correlation
this pattern is likely to be predictable in terms of
a certain weight time leading to a certain percentage A
while back we mentioned that our values aren't often whipped
up by hand Instead we use graphing calculator spreadsheets websites
any of them you know to whip up a mess
of our values in no time Pop the data into
the list one into in a t i a graphing
calculator Go to the count menu in the stat function
and run a lynn rag Linear regression You know we
see in our value of ours a negative point eight
nine one which is very close to our by the
hand value of point eight nine hundred eleven year negative
and is on ly different dude around it So yeah
when you need to rustle up in our value y'all
should probably grab something Check unless you want to go
through the headache of finding that our value by hand
remember that the r value just suggests a relationship between
the variables revenues saying one causes the other correlation does
not equal causation Remember that tattoo that somewhere but not
on your own body Also remember that the stronger correlations
air closer to negative one in one and farther from
zero in the middle And finally when they all go
to a restaurant and takes a spell get your order
Don't take it out on the server by stiffing them
on the tip There's a strong positive correlation between stiffing
service on tips and you know getting your food spat
in next time And while just being a massive
Up Next
What is inverse correlation? An inverse correlation is a relationship between two variables in which one moves in the opposite direction to the oth...
